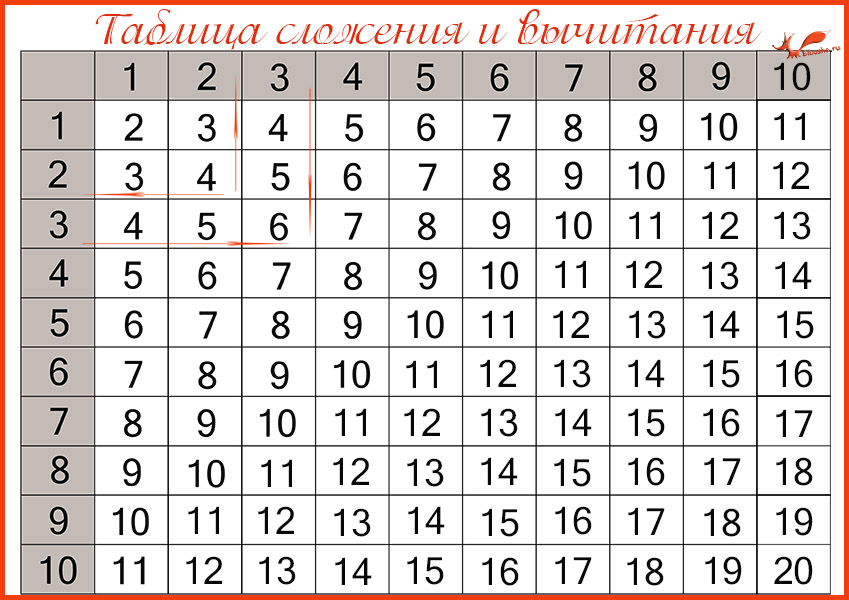
Как научить ребенка делению во 2 классе?

Вместо заключения

Уделяйте математике достаточно внимания уже с начальной школы. Этот предмет не только тренируем мозг в устном счете, но и умении логически мыслить, развивать смекалку. Постепенно привыкая к выполнению дополнительных и основных заданий, ребенок учится учиться, выполнять требования учителя, грамотно планировать свое время, распределять время для учебы и досуга.

Математические задания для третьеклассников моно составлять самостоятельно по приведенным нами аналогии, это не составит особого труда. Зато ваш ученик сможет больше тренироваться в математике, выполнять задания на каникулах и выходных, а также заниматься дополнительно после школы.

Деление двузначного числа на однозначное

Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.

Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.

Устное деление двузначного на однозначное

Задание 1.

Пусть надо решить, сколько будет

К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.

Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.

Все понятно? Будем тренироваться.

Задание 2.

Задание 3.

Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.

Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.

Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.

Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.

Решите задачу.

Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?

Чтобы ответить на вопрос задачи, надо выполнить действие деления.

96 : 4 =

«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.

Ответ: 24

Этап пройден. Вот вам синяя лента в награду.

Деление столбиком двузначное на однозначное

Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.

Задание 1.

Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.

Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.

Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.

8 – 1 = 7. В таблице нет деления семи на три.

Уменьшаем еще на 1.

7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.

Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.

А надо было разделить восемь.

Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.

Давайте проверим: два меньше трех.

Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.

После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое

Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24

Ответ: 28.

Задание 2.

Решите пример столбиком 96 : 4 =

Проверьте:

Ребята, вы молодцы. Ловите последнюю награду — фиолетовую шелковую полоску.

Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:

Да какая разница?

Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?

Рассмотрим примеры:

10 – 5 + 2 = ?

Если мы будем выполнять действия по порядку, получим:

1. 10 – 5 = 5;
2. 5 + 2 = 7.

Попробуем иначе:

1. 5 + 2 = 7;
2. 10 – 7 = 3.

Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:

25 – (18+2) = ?

Пробуем решить двумя способами:

1. 25 – 18 + 2 = 9;
2. 25 – 20 = 5.

Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:

1. 18 + 2 = 20;
2. 25 – 20 = 5.

Другого решения у ответа у примера быть не должно.

Итак:

Правило первое: Математические действия в выражении выполняются по порядку, начиная с левого, направо.
Правило второе: Если в выражении есть скобки, действие в скобках выполняется в первую очередь, а затем следуют действия по порядку, слева направо.

1 Объясняем ребенку деление в форме игры

Отложите в сторону скучные учебники. Превратите обучение в интересную игру:

• возьмите яблоки или конфеты. Попросите малыша, чтобы он разделил между двумя-тремя куклами или мишками четыре конфетки или яблока. Постепенно увеличивайте количество фруктов до восьми и десяти. Сначала ребенок будет раскладывать предметы медленно. Не кричите на него, запаситесь терпением. Если ошибается – спокойно поправьте. После того, как игрушки «получат» конфеты, пусть ребенок посчитает, сколько у каждой куклы их получилось. Подведите итог. Если было 6 конфет и их раздали трем куклам – каждой досталось по две. Объясните, что «разделить» – это значит, что всем нужно раздать поровну;
• другой игровой пример. Объясняем деление на цифрах. Скажите ребенку, что цифры являются теми же яблоками или конфетами. Объясните ему, что количество конфет, которое нужно разделить называется делимое. А количество человек, на которых делятся конфеты – делитель;
• дайте малышу 6 яблок. Попросите, чтобы он раздал их поровну бабушке, кошке и папе. Потом пусть он поделит это же количество предметов между котом и бабушкой. Объясните, почему получился разный результат;
• объясняем деление с остатком. Дайте малышу 5 орехов, и пусть он угостит в одинаковом количестве ими папу и бабушку. Оставшийся орешек малыш забирает себе. Объясните на этом примере, что один орешек и является остатком.

Вышеуказанные способы в игровой форме помогут ребенку понять процесс деления и то, что большее число делится на меньшее. Первое число – это количество яблок или конфет, а число второе – участники, между которыми делятся предметы. Для ребенка в возрасте от 5 до 8 лет этой информации хватит. Учите делению малыша еще до школы, ему будет легче усваивать уроки математики в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью  переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

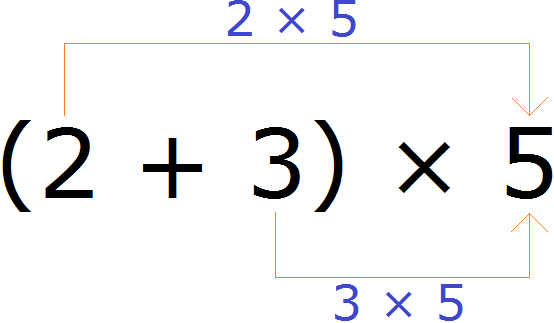
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают короче:  −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

2 × 3 = 6

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно решение записывают покороче:

12 × (−5) = −60

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Запишем решение покороче:

10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Запишем решение покороче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

4 × (−2)

Заключим его в скобки:

( 4 × (−2) )

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

( 4 × (−2) ) + ( (−4) × (−2) )

Всё это приравняем к нулю:

(4 × (−2)) + ((−4) × (−2)) = 0

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))

−8 + ((−4) × (−2)) = 0

Теперь вместо второго произведения временно поставим многоточие

−8 + … = 0

Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

−8 + 8 = 0

Пример 5. Найти значение выражения  −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число  −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = −2 × 6 + (−2) × 4

Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

Первое действие:

−2 × 6 = −12

Второе действие:

−2 × 4 = −8

Третье действие:

−12 + (−8) = −20

Значит значение выражения −2 × (6 + 4) равно −20

Запишем решение покороче:

−2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

(−2) × (−3) = 6

Второе действие:

6 × (−4) = −(6 × 4) = −24

Значит значение выражения (−2) × (−3) × (−4) равно −24

Запишем решение покороче:

(−2) × (−3) × (−4) = 6 × (−4) = −24

Деление целых чисел

Пример 1. Найти значение выражения 12 : (−2)

Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.

12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6

Обычно записывают покороче:

12 : (−2) = −6

Пример 2. Найти значение выражения −24 : 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.

−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4

Запишем решение покороче:

−24 : 6 = −4

Пример 3. Найти значение выражения −45 : (−5)

Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

−45 : (−5) = |−45| : |−5| = 45 : 5 = 9

Запишем решение покороче:

−45 : (−5) = 9

Пример 4. Найти значение выражения −36 : (−4) : (−3)

Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим −36 на (−4), и полученное число разделим на −3

Первое действие:

−36 : (−4) = |−36| : |−4| = 36 : 4 = 9

Второе действие:

9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3

Запишем решение покороче:

−36 : (−4) : (−3) = 9 : (−3) = −3

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Умножение суммы на число

Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?

Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:

Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.

Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.

Таким способом удобно умножать большие величины.

Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.

Умножайте сначала десятки, потом единицы, произведения складывайте.

Как это сделать, рассмотрите на примере.

Сумму десяти и пяти умножим на шесть.

Это распределительное свойство умножения суммы на число.

Правило умножения суммы на число запишите буквенным выражением.

За внимание награждаю вас оранжевой лентой

Идите по маршруту дальше.

Что нужно для освоения деления в младшем школьном возрасте

Деление это не первое арифметическое действие, которое осваивают дети. Поэтому, прежде чем браться за делимое-делитель-частное, нужно обязательно выяснить, знает ли ребёнок разряды чисел и понимает ли принципы:

• сложения;
• вычитания;
• умножения.

Эффективные способы объяснения деления школьникам

Все способы объяснения можно условно поделить на академичные и образные. Первые опираются на цифры, то есть записываются в виде арифметических примеров, вторые на конкретные предметы: конфеты, мячи и т. д., которые умозрительно делятся между людьми, игрушками.

В работе с учениками начальной школы эффективным будет синтетический способ, совмещающий опору на образы и цифры одновременно.

Деление на основе знания таблицы умножения

Для понимания сути деления стоит обратиться к вычислениям с опорой на таблицу умножения.

Инструкция:

1. Записываем пример: 2 х 5 = 10.
2. Берём 10 монет и просим поделить их на двоих получается две стопки по 5 монет.
3. Далее 10 монет делим на пятерых получается 5 стопок по 2 монеты.
4. Вывод при делении мы выясняем, сколько раз каждый множитель помещается в произведении.

На этом приёме разъясняем понятийную базу: то число, которое делится, называется делимое, то число, на которое делится делителем, а результат частным.

Поскольку деление обратно умножению, то второе может проверить результат первого.

Инструкция:

1. Делимое делим на делитель, то есть 10 : 2.
2. Получаем частное 5.
3. Проверяем умножением, то есть частное умножаем на делитель 5 х 2.
4. Получаем 10, что в исходном примере является делимым.

Деление двузначных чисел на однозначные

Чтобы разделить двузначное число, не являющееся произведением таблицы умножения, на однозначное, нужно каждую цифру делимого разделить на делитель и записать первое частное десятками, а второе единицами. Например, 86 : 2.

Инструкция:

1. Делим 8 на 2. Получаем 4.
2. Делим 6 на 2. Получаем 3.
3. Ответ 43.
4. Проверяем 43 х 2 = 86.

Деление способом группирования

Суть этого способа деления заключается в подсчёте количества групп равных делителю, которые помещаются в делимое. Результат будет частным.

Инструкция:

1. Задача состоит в распределении мячей между командами. Решаем пример 30 : 3.
2. Распределим 30 мячей между тремя командами обводим тройки.
3. Считаем количество групп троек 10. Каждой команде достанется по 10 мячей.
4. Вывод 30 : 3 = 10.

Как объяснить деление в столбик

Поскольку деление может быть без остатка, а может быть с остатком, рассмотрим два варианта объяснение такого арифметического действия.

Деление без остатка

Инструкция:

1. Решим пример 396 : 3.
2. Записываем делимое, справа рисуем повёрнутую на левый бок букву Т и в верхнем окошке вписываем делитель 3.
3. Начинаем с сотен. 3 делится на 3 без остатка, получаем 1. Вписываем результат под делителем.
4. Проверяем 1 х 3 получаем 3, вписываем 3 под сотней и производим вычитание. Остатка нет. Подводим черту.
5. Приступаем к десяткам. 9 : 3 получаем 3. Записываем 3 рядом с 1.
6. Проверяем 3 х 3 получаем 9, вписываем 9 под чертой, производим вычитание. Остатка нет. Подводим черту.
7. Работаем с единицами. 6 : 3 получаем 2. Записываем 2 рядом с 13.
8. Проверяем 2 х 3 получаем 6, вписываем 6 под чертой, вычитаем. Остатка нет.
9. Результат 132.

Деление с остатком

Инструкция:

1. Решим пример 90 : 4.
2. В десятках помещается две четвёрки. В частном запишем значение 2, затем перемножаем 2 х 4 = 8, вписываем под 9 полученное произведение, вычитаем и получаем 1.
3. Сносим к разности 0, получаем 10. В 10 помещается 2 четвёрки, 10 8 = 2. Это остаток.
4. 2 на 4 не делится. Ставим десятичную запятую в частном и добавляем 0 к 2.
5. 20 : 4 = 5. Записываем частное после запятой.
6. Проверяем умножением 5 х 4 = 20. 20 20 = 0 остатка нет.

Деление на двузначные числа

Если в делителе есть десятки, сотни, то для облегчения решения делитель можно упростить, разбив на единицы (десятки).

Инструкция:

1. Решим пример 405 : 15.
2. Разобьём 15 на единицы, на 5 и 3 их произведение равно 15.
3. Теперь решаем два примера. Сначала 405 : 5. Частное 81.
4. Затем 81 : 3. Частное 27.
5. Результат 405 : 15 = 27.

Видео: тренажёр быстрого деления в уме для школьников

Объяснить деление можно не только школьнику, но и дошкольнику. Причём не только в условиях детского сада, школы, но и дома. Для этого нужно убедиться, что ребёнок имеет опорные знания, и у родителя есть запас времени, терпения для регулярных занятий со своим чадом.

Как учить ребенка учиться

Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.

А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.

Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.