Искусство умножения двузначных чисел в уме

Как объяснить принцип работы в таблице умножения

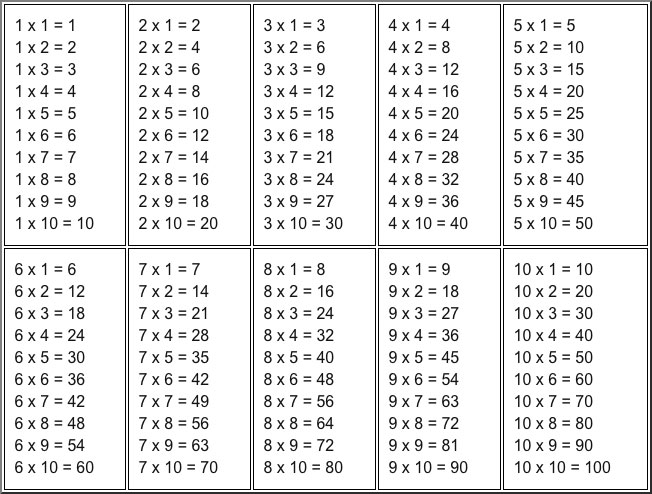
Когда ребёнок изучает таблицу умножения по таблице Пифагора, ему проще увидеть закономерность и симметрию в таблице умножения, и в этом случае он просто запомнит её на всю жизнь, в отличие от простой таблицы, где столбики с примерами. Для ребёнка нужно постараться превратить процесс изучения таблицы умножения в занимательную игру.

После этого нужно начать разбирать процесс устройства таблицы Пифагора. Самое главное в этом процессе показать, что если взять число из левого столбика и умножить его на число из верхней строки, то правильный ответ нужно искать на месте их пересечения. Для этого нужно провести рукой или карандашом по таблице точке пересечения.

Скорее всего, за один раз ребёнок не сможет понять и выучить всё. Для начала нужно начать с колонок 1, 2 и 3, и учить небольшими порциями. Делая так, вы сможете подготовить ребенка к изучению и усвоению таблицы умножения и в другой более сложной информации. После изучения с ребенком азов, можно воспользоваться следующей методикой. Нужно взять пустую нарисованную таблицу Пифагора, и объяснить, как заполнить её самостоятельно. Можно начать с небольшого участка таблица умножения, чтобы ребёнок не запоминал, а учился считать.

Когда ребёнок понял и разобрался, то есть хорошо усвоил самые первые и простые столбцы, правила их умножения, можно перейти  к числам более сложным, сначала к правилу умножения цифр с 4 до 6, и уже после этого умножение чисел от 8 до 10.

На что еще обратить внимание при изучении таблицы умножения с ребенком

Нужно чтобы родители рассказали ребёнку, что такое свойство коммутативности. Это математическое правило о том, что от перестановки множителей произведение не меняется. Если ребёнку правильно и просто объяснить это правило, и показать на конкретных примерах, то ребёнок быстро поймет, что всё не так сложно, и нужно учить на самом деле не всю таблицу умножения, а только её часть. Например, 3 умножить на 7 — это то же самое, что и 7 умножить на 3. То есть, когда он перейдет к изучению крайних столбцов таблицы, умножение чисел в них, он поймёт, что многие примеры по умножению чисел он уже знает. Это очень обрадует ребёнка.

Закономерности в таблице умножения

При изучении таблицы умножения нужно знать и обратить внимание на закономерности в ней, они помогут и упростят запоминание таблицы Пифагора. Рассмотрим некоторые примеры

Если умножить число 1 на любое другое число, то она останется тем же самым. При работе с числом 5 все примеры будут оканчиваться на 5 или на 0. Если число четное, то нужно приписать 0 половине числа, если нечетное, то 5.

Примеры с участием числа 10 заканчиваются на ноль, а начинается с того числа, на которые мы делаем умножение.

Все примеры на 5 меньше чем примеры на 10, например 5 умножить на 10 равно 50, а 5 умножить на 5 равно 2 раза меньше, то есть 25.

При изучении умножении чисел на девять, можно научить ребенка такой закономерности. Нужно записать ответы умножения чисел на 9 в столбик, то есть 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Нужно запомнить самое первое и самое последнее число, То есть 09 и 90. Все остальные числа между ними можно написать и вспомнить по следующему правилу, первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1. То есть, после 09 будет идти число 18, 0 + 1 это 1, а 9 — 1 это 8. И так далее.

Обязательно нужно заниматься с ребёнком, постоянно повторять таблицу умножения. Для начала, когда ребёнок ещё только в процессе изучения, спрашивайте примеры по порядку. Когда же вы заметите, что ребёнок стал отвечать уверенно, то можно спрашивать разброс. Обычно в начале изучения ребенку требуется больше времени на размышления, однако потом можно увеличивать темп и уменьшать время на размышление.

Правила

Царица наук – математика – позаботилась о школьниках и составила свод законов, алгоритмов и правил, усвоив которые и умело ими пользуясь, дети полюбят математику и умственный труд:

• Переместительное свойство сложения: меняя местами компоненты действия, получаем тот же результат.
• Сочетательное свойство сложения: при складывании трех и более чисел любые два (или больше) числовые значения можно заменить их суммой.
• Сложение и вычитание с переходом через десяток: дополнить больший компонент
• До круглых десятков, а потом прибавить остаток от другого компонента.

• Вычитаем вначале отдельные единицы из числа до знака действия, а далее из круглых десятков вычитаем остаток вычитаемого.
• Представив уменьшаемое в виде суммы десятков и единиц, уберем из десятков большего меньшее и прибавим к ответу единицы уменьшаемого.
• При складывании и вычитании круглых десятков (их еще величают «круглые» числа) десятки можно считать так же, как единицы.
• Сложение и вычитание десятков и единиц. Десятки удобнее прибавлять к десяткам, а единицы — к единицам.

Прибавление числа к сумме

Способы следующие:

• Вычисляем ее значение, а затем прибавляем к ней данную величину.
• Прибавляем его к первому слагаемому, а затем к результату прибавляем второе слагаемое.
• Число прибавляем ко второму слагаемому, а затем к ответу прибавляем первое слагаемое.

Прибавление суммы к числу

Способы следующие:

• Вычислим ее показание, а затем прибавим к числу.
• К числу прибавим первое слагаемое, а затем к результату прибавим второе слагаемое.
• К числу прибавим второе слагаемое, а затем к результату прибавим первое слагаемое.

Использование главных свойств умножения

Методики таковы:

• Переместительное свойство умножения. Если поменять сомножители местами, их произведение не изменится.
• Сочетательное свойство умножения. При перемножении трех и более чисел любые два (и больше) числа можно заменить их произведением.
• Распределительное свойство умножения. Чтобы умножить сумму на число, надо умножить каждое ее составляющее на это число и полученные произведения сложить.

Умножение и деление чисел на 10 и 100

Способы:

• Чтобы увеличить любое число в 10 раз, надо приписать к нему справа один ноль.
• Чтобы это же сделать в 100 раз — надо приписать к нему справа два ноля.
• Чтобы уменьшить число в 10 раз, надо отбросить справа один ноль, а чтобы разделить на 100 — два ноля.

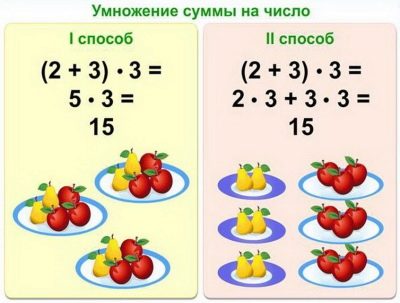
Умножение суммы на число

Способы:

• 1-й способ. Посчитаем сумму и умножим ее на данную величину.
• 2-й способ. Перемножим число с каждым из слагаемых, и полученные ответы сложим.

Умножение числа на сумму

Способы:

• 1-й способ. Найдем сумму и умножим число на то, что получим.
• 2-й способ. Умножим число на каждое из слагаемых, и полученные произведения сложим.

Деление суммы на число

Способы:

• 1-й способ. Вычислим сумму и разделим ее на число.
• 2-й способ. Каждое из слагаемых разделим на число и полученные частные сложим.

Деление числа на произведение

Варианты:

• 1-й способ. Разделим число на первый множитель, а затем полученный результат разделим на второй множитель.
• 2-й способ. Разделим число на второй множитель, а затем полученный результат разделим на первый множитель.

Небольшие секреты, которые должен знать каждый

1. Умножая на 1, числа не меняются – это одно из простейших правил в математике.
2. При умножении на 5, числа будут заканчиваться на 0 или 5. 0 получает при умножении чётных чисел, а 5 ‒ нечётных.
3. Умножая на 10, просто дописывайте нолик к числу, которое умножаете.
4. Умножая на 4, необходимо каждый раз удваивать полученное число, например: 7 + 7= 14 и 14+14= 28.

Не оставляйте ребенка с проблемами, уделяйте время и старайтесь разобраться в сложностях, которые вызывает таблица умножения. И помните, выучить таблицу умножения за 5 минут невозможно, но можно развить в ребенке любовь к точным наукам, ведь первое знакомство малыша со сложной математикой начнётся именно с таблицы умножения.

Как считать чаевые в процентах

Быстрое определение суммы чаевых – обязательная мера в кафе или ресторане

Иногда в заведениях общепита уже заложены чаевые и тут важно быстро считать, чтобы пользователя не обманули

Например, вычисление 7% от 300 делают так:

• раскладывают большое число на сотни;
• из каждой 100 считают 7%, это 7;
• складывают количество высчитанных процентов по количеству сотен = 7+7+7 = 21.

Итого 7% от 300 = 21. Точно таким же образом считают все проценты. Поняв, что 1% из 100 равен 1, легко вычислить необходимую сумму выплат. Например, 5% от суммы чека в 1650 рублей составят: (5% от 1000 = 50) + (5% от 600 = 30) + (5% из 50 = 2,5) = 50+30+2,5 = 82,5 рубля. Итого сверх суммы обеда чаевые полагаются не более 82,5 руб.

Вот и все премудрости. Зная их, взрослый никогда не ошибется в сдаче на кассе, рынке. Также будет просто объяснить правила математики малышу.

Как ребенку научиться быстро считать в уме:

• тренироваться каждый день вместе с родителями;
• считать собственные деньги, затраты.

Тут многое делают родители, отправляя ребенка в магазин и поручая считать сдачу. Быстрее всего учатся считать на деньгах. И именно эти знания затем пригодятся в жизни.

Приемы устного счета

Признаки делимости чисел:

• на 2: все, что превышают его, и в числовом ряду идут через одно;
• на 3 и 9: если сумма цифр кратна этим показателям без остатка;
• на 4: если две последние цифры в записи последовательно образуют число, которое подвергается делению на 4;
• на 5: круглые десятки и те, где на конце стоит 5;
• на 6: делятся числа, которые кратны двойке и тройке;
• на 10: числовые значения, в записи которых на конце стоит 0;
• на 12: делятся числа, которые можно разделить на тройку и четверку одновременно;
• на 15: числа, которые делятся одновременно на целые однозначные составляющие это число множители.

Секреты устного счёта

Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.

Прибавляем числа 7,8,9

Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.

Примеры:

56+7=56+10-3=63

47+8=47+10-2=55

73+9=73+10-1=82

Быстро складываем двузначные числа

Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».

Примеры:

54+39=54+40-1=93

26+38=26+40-2=64

Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.

Пример:

57+32=57+30+2=89

Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:

32+57=32+60-3=89

Складываем в уме трехзначные числа

Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.

Пример:

249+533=(200+500)+(40+30)+(9+3)=782

Особенности вычитания: приведение к круглым числам

Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.

Примеры:

67-9=67-10+1=58

576-88=576-100+12=488

Вычитаем в уме трехзначные числа

Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.

Пример:

843-596=843-500-90-6=343-90-6=253-6=247 

Умножить и разделить

Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!

Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:

15*16=15*10+(10*6+5*6)=150+60+30=240

Умножаем и делим на 4, 6, 8, 9

Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.

Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:

• умножить на 4 — это дважды умножить на 2;

• умножить на 6 — это значит умножить на 2, а потом на 3;

• умножить на 8 — это трижды умножить на 2;

• умножить на 9 — это дважды умножить на 3.

Например:

37*4=(37*2)*2=74*2=148;

412*6=(412*2)·3=824·3=2472

Аналогично:

• разделить на 4 — это дважды разделить на 2;

• разделить на 6 — это сначала разделить на 2, а потом на 3;

• разделить на 8 — это трижды разделить на 2;

• разделить на 9 — это дважды разделить на 3.

Например:

412:4=(412:2):2=206:2=103

312:6=(312:2):3=156:3=52

Как умножать и делить на 5

Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.

Пример:

326*5=(326*10):2=3260:2=1630

Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.

326:5=(326·2):10=652:10=65,2.

Умножение на 9

Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:

37*9=(37*3)*3=111*3=333

или

37*9=37*10 — 37=370-37=333

Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

2. Умножаем каждый кусочек на второе число.

3. Разбиваем результаты на простые группы одного размера.

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 6000 + 1000 + 40 + 8

27048

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

С чего начать изучение таблицы умножения?

Первый этап подготовки выполните сами – распечатайте таблицу Пифагора и таблицу с примерами

И вот тут важно обратить внимание, что это не одно то же. Во втором случае это просто примеры с готовыми ответами, представленные в столбиках для каждой цифры. Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10

Первый вариант и является настоящей таблицей умножения (Пифагора), которая представлена сеткой 10х10.

Прежде чем выучить наизусть всю таблицу умножения ребенку, покажите ему, что цифры, которые перемножаются, находятся слева и сверху, а если пальчиками от них провести навстречу друг другу, то на пересечении будет результат их перемножения.

Задаваясь вопросом, как быстро выучить таблицу умножения ребенку, и с чего начать этот процесс, то знакомить его с самими действиями нужно, начиная с тех манипуляций с умножением, которые ему понять и выполнить самостоятельно будет проще всего:

• На «1». Любое действие в этом случае дает результат, при котором число остается прежним. Так школьнику будет проще понимать, что это за процесс. Предложите ему попрактиковаться с умножением на один несколько раз с разными числами;
• На «10». Объясните ребенку, что, несмотря на то что это большое число, умножать на него очень просто. Нужно лишь к умножаемому приписывать ноль. Начните с небольших значений – например, 3х10, а потом предложите ему самостоятельно попробовать выполнить действия с большими числами.

На пути к тому, как научить быстро выучить таблицу умножения ребенка, это важные шаги. Теперь он знает, как работать с крайними значениями сетки Пифагора. Помимо практического значения, для него это играет и психологическую роль:

• У школьника сложится понятие того, как нужно работать с ней;
• Он поймет, что начало положено, и ему знакомиться с сеткой не сложно, даже интересно, поэтому полностью ее освоить он сможет.

Если ученик еще не устал, можно приступать к следующему этапу того, как можно быстро выучить таблицу умножения:

Предложите школьнику умножать на «2». Уже с первых классов обучения математике дети знают, как выполнять сложение до 10, в том числе одинаковых чисел. Поэтому занятие будет для обучаемого простым и даже интересным;
Перемена мест множителей

Это важное правило, часто непонятное детям, заключающееся в том, что при перестановке множителей их произведение остается прежним. Обязательно покажите это на самой сетке в соответствующих графах

Благодаря этому ребенку проще будет запомнить это правило, называемое коммутативным или переместительным. К тому же, так он быстрее запомнит определенные действия умножения и их произведения.

Это первые шаги, применяя которые вы положите начало запоминанию и к тому, чтобы быстро и просто потом выучить действия и результаты, указанные в сетке.

как выучить таблицу умножения

Подготовка к изучению таблицы умножения

Этот этап является в том числе организационным, но он входит в алгоритм того, как быстро и просто выучить таблицу умножения. Подготовка включает в себя такие шаги:

• Подберите время, когда вы ежедневно будете заниматься с ребенком. Учитывайте, что на изучение нужно уделять не менее 30 минут (это длительность одного занятия). Поэтому в это время ученик не должен быть уставшим, но должен быть готов к эффективному обучению;
• Приготовьтесь к тому, что процесс этот должен включать игровой момент, потому что так ученику гораздо проще запомнится этот материал;
• Саму сетку или столбики с примерами вы можете распечатать, а можете расчертить самостоятельно;
• Продумайте, как и когда, в какое время вы будете проверять выученный материал.

Система охлаждения ваз 2110

Вам нужна только математика начальной школы

Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

I. Знать таблицу умноженияII. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Действие умножения

Если понимать, что умножение – это сложение одинаковых чисел определенное количество раз, ничего сложного в действии нет. Например, 4*7 = 4+4+4+4+4+4+4. В итоге получают 28. Упростит действие таблица умножения. Ее знает каждый школьник.

Чтобы правильно умножать числа, их сводят к простым. Рассмотрим техники умножения.

Умножение 9 и 11

Правило при умножении на 9 умножают на 10 и вычитают 9. Если умножают на 11, сначала умножают на 10, прибавляя исходный показатель.

Пример:

• 15*9 = 15*10-15 = 150-15 = 135;
• 57*11 = 57*10+57 = 570+57 = 627.

Умножение на 5 чисел до 10

Эта техника поможет правильно умножать двух-, трехзначные числа. Правило простое – множитель делят на 2. Получив результат в виде целого показателя, добавляют в конце 0, а если число не целое, отбрасывают остаток и добавляют в конце 5.

Пример 1482*5 решают так:

• (1482/2) _ (+0 или +5) = 741 _ (+0) = 7410 – исходный показатель делили на 2 без остатка;
• 2269-5 = (2269/2) _ (+0 или +5) = 1134,5 _ (+5) = 11345 – исходный показатель делили на 2 с остатком.

Техника, как быстро научиться считать деньги, умножая число на 5, 25, 50, 125 с использованием формул:

• А*5 = А*10/2;
• А*50 = А*100/2;
• А*25 = А*100/4;
• А*125 = А*1000/8.

Приставляя вместо А цифру, в процессе решения формулы получают нужный результат. Например, 25*25 = 25*100/4 = 2500/4 = 625.

Умножение больших чисел с одним четным

В этом случае пользуются методикой упрощения множителей. Четное число уменьшают в 2 раза, а нечетное увеличивают в 2 раза. Например, 48*125 = 24*250 = 12*500 = 6*1000 = 6000.

Умножение многозначного числа на однозначное

Разбираясь, как научиться быстро считать деньги на кассе, пользуются техникой раскладывания на порядки, как в случае сложения. Пример 468*6 решают так:

1. Раскладывают 468 на 400, 60, 8. Умножают каждое число на 6.
2. Получают (400*6) = 2400 + (60*6) = 360 + (8*6) = 48. Итого 2400+360+48 = 2808.

Более сложный вариант с перегруппировкой итоговых результатов выглядит так: 2400+360+48 = 2000+400+300+60+48 = 2000+700+108 = 2808.

Умножение простых чисел

Диагональный метод нужен при поисках техники как быстро научиться считать устно. Заключается способ в дописывании числа, которого «не хватает до 10».

Пример 7*8 решают так:

• высчитают недостающее до 10 – в 7 это 3, в 8 это 2;
• затем 8-3 = 5;
• 3*2 = 6;
• в итоге получают 56.

Умножение чисел от 10 до 20

Правило – к одному числу прибавляют единицы другого, а сумму умножают 10. К результату добавляют сумму единиц. Например, 13*15 = (13+5)*10 + 3*5 = 180+15 = 195.

Умножение двузначных чисел

Упрощают процесс снова разложением двузначных чисел на простые действия. Пример 78*56 решают так:

1. В итоге должно получиться сложение цифры 78 точно 56 раз. Сначала складывают 78 пятьдесят раз, затем еще 6 раз.
2. Считают 78*5 = 70*5 + 8*5 = 350+40 = 390*10 = 3900.
3. 78*6 = 70*6 + 8*6 = 420+48 = 468.
4. 3900+468 = 3000+900+400+60+8 = (3000+1300+60+8) = 4368.

Пользуясь принципом упрощения и раскладывания больших чисел на разряды, умножают все двузначные числа.

Умножение на 9, 99, 999

Учитывают правило прибавления недостающих единиц. Пример 154*99 решают так: 154*(100-1) = 15400-154 = 15246. Таким же образом умножают на 9, 999.

Возведение в квадрат

Это тоже умножение, при котором число раскладывают на составляющие. Сначала находят произведение первой цифры на следующую за ней, результат будет заканчиваться на квадрат последней цифры. Пример возведения 75 в квадрат решают так: 7*8 = 56; 5*5 = 25. В итоге 75*75 = 5625.

Как научить ребенка?

Многие родители задаются вопросом, с какого возраста нужно начинать обучать счету? Чем раньше, тем лучше! Обычно первый интерес проявляется у детей в возрасте 5-6 лет, а иногда и раньше, главное не упустить и начать развивать. Считайте все, что придет вам в голову – птичек на ветке, машины на стоянке, люди на лавке или цветочки в грядке. Считать можно любимые игрушки, обязательно обзаведитесь развивающими наборами кубиков с цифрами, переставляйте, проводите первые операции сложения и вычитания на зрительном примере.

Вообще в детском возрасте все должно напоминать игру: например, есть замечательная развивайка «гномики в домике». Придумайте картонную коробку – это будет домик. Возьмите несколько кубиков – объясните ребенку, что это гномики. Поместите в домик одного гномика и скажите – «в домик пришел один гномик». Теперь у ребенка нужно спросить, если в гости к гномику придет еще один, то, сколько теперь гномиков окажется в домике?

Не ждите правильных ответов сразу, но, как только услышите правильный – разместите нужное количество кубиков в коробке, чтобы ребенок не только в уме, но и зрительно видел реальный результат действия. Это и есть первые способы, как развивать в ребенке умения считать в уме.

Таблица умножения на 3

Объясните умножение на 3 в том же порядке, но тут придется посидеть подольше, ведь умножения на число 3 вызывает сложности. Воспользуйтесь игровой формой, либо найдите песни и стихи. Лучший пример – воспроизвести таблицу умножения на 3 с помощью бытовых предметов, которые окружают ребенка. Это вызовет ассоциации, и ученик будет быстрее воспринимать информацию. Используя ручки и карандаши, которые малыш всегда берет с собой в школу, в случае контрольной, метод ассоциаций придет на выручку.  Вспомнив, что 3 карандаша + 3 карандаша + 3 карандаша, он получил цифру 9. Визуальное запоминание информации остается одним из самых эффективных методов учебы.

Таблица со стихами придет на помощь, если другие способы не сработали.

Самые интересные приемы

Чтобы увлечь детей математикой и сделать трудные моменты в школьной программе ближе и доступнее, существуют способы и методические приемы, превращающие сложности в забавное и интересное:

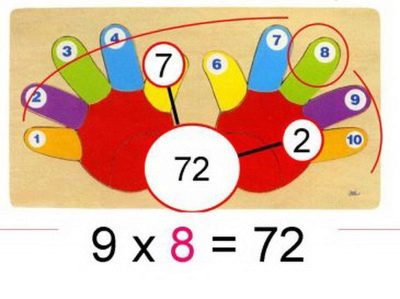
• Чтобы умножить любое однозначное число на 9, покажем всем свои пустые ладони. Загнем палец, соответствующий по порядку (считая от большого пальца левой руки) числу первого сомножителя. Смотрим, сколько пальцев слева от загнутого — это будут десятки искомого произведения, а справа — его же единицы.
• Умножение на 11 любого двузначного числа, сумма цифр которого не достигает 10, осуществляется забавно и просто: мысленно раздвинем цифры этого числа и поставим между ними их сумму — ответ готов.
• В случае, если сумма цифр умножаемого на 11 числа окажется равна 10-ти или более 10-ти, то между мысленно раздвинутыми цифрами этого числа следует поставить их сумму и сложить первые две цифры слева, оставив две другие без изменения, – получили произведение.

О том, как научить ребёнка моментально считать в уме, смотрите в следующем видео.

Игра

В любом даже рутинном процессе, коим являются и упражнения для изучения таблицы умножения, должен обязательно присутствовать элемент игры, он необходим для детей! Обучение с привлечением игровых приемов заставит ребенка вникнуть в задание, по-настоящему заинтересоваться предметом умножения и забыть о нежелании учиться. Одно из главных правил запоминания гласит: интересное запоминается лучше и быстрее. Если вы сможете пробудить интерес ребенка к умножению, вы уже сделаете половину дела!

Одной из популярных игр изучения таблицы умножения, является игра в карточки. Подробнее об игре «» вы можете прочитать в этой статье, в также скачать и распечатать уже готовые карточки с примерами и ответами. Суть этой игровой таблицы умножения заключается в том, что ребенок в случайном порядке вытягивает карточку из стопки и видит на каждой карточке пример умножения без ответа (например, 7×7=? или 3×8=?). Если он дает правильный ответ, то карточка «выходит из игры», а если ответ неверен, то карточка возвращается в самый низ стопки, и может быть вытянута снова. Игра продолжается до тех пор, пока не закончатся все карточки, то есть пока ребенок не даст правильный ответ на все примеры. Когда карточек остается мало, как правило, это трудные примеры, которые ребенок уже пытался решить, то путем повторения они достаточно легко запоминаются, особенно когда в процессе игры у ребенка появляется азарт.

Эту игру иногда называют «тренажер таблицы умножения». Весь игровой процесс можно проводить этапами, в зависимости от выученного материала. Например, можно начать свой импровизированный урок с карточек «таблица умножение на 2», а потом разбавлять их новыми выученными примерами. Вариантов игры множество, в чем вы можете убедиться сами.

Кроме того, привнести элемент игры в изучение таблицы умножения вы сможете, используя всевозможные программы, онлайн-игры, специальные звуковые плакаты и многое другое, что без проблем можно найти в интернете. Но игра «карточки для запоминания таблицы умножения» является наиболее простым и эффективным способом выучить Пифагорову таблицу.

Устаревшая математика?

В блестящем TED-выступлении в октябре 2014 года Эдуардо Саенц де Кабесон сказал: «Если вы хотите сделать подарок навечно, не дарите бриллианты, подарите теорему!»

Если математический результат доказан, то он верен всегда. Любая теорема — на века. В других науках это не так. Например, сначала люди считали, что земля плоская; потом стали полагать, что круглая. Сначала думали, что брожение вина — это химический процесс, потом Луи Пастер доказал, что брожение происходит из-за бактерий (кстати, именно в честь Пастера мы называем молоко пастеризованным). Математика в этом плане занимает особенное место.

Тем не менее, в математике, как в искусстве, что-то становится классикой, а что-то устаревает. Например, теорема Пифагора — это золотая классика, которая не устареет никогда! Не случайно профессор математики и популяризатор Алексей Савватеев сказал, что именно эту теорему он передал бы в капсуле инопланетянам как одно из основных достижений человеческого разума.

Что же такое устаревшая теорема? Нелли запомнилась история, которую ей рассказал коллега из университета Твенте, профессор по вычислительным методам.

Вычислительные методы — это область математики, которая разрабатывает алгоритмы, чтобы решать задачи приблизительно, с помощью вычислений, а не с помощью формул. Коллега Нелли рассказал ей, как лет двадцать назад уходил на пенсию старый профессор и оставил ему журналы по вычислительным методам 60-х годов. Это были отличные журналы, в них публиковались известные авторы. Но только тогда еще не было общедоступных быстрых компьютеров. Ученые пользовались так называемыми специальными функциями и таблицами, которые занимали целые тома.

С появлением компьютеров все изменилось, потому что машины считают очень быстро. Обычный ноутбук выполняет 2 миллиарда операций в секунду! Многие результаты и подходы докомпьютерной эпохи безнадежно устарели. Коллега Нелли глубоко вздохнул и отнес все эти журналы в макулатуру.

Быстрое определение необходимого минимума

Представьте, что вы проходите серию из пяти тестов, для успешной сдачи которых вам необходим минимальный балл 92. Остался последний тест, а по предыдущим результаты таковы: 81, 98, 90, 93. Как вычислить необходимый минимум, который нужно получить в последнем тесте?

Для этого считаем, сколько баллов мы недобрали/перебрали в уже пройденных тестах, обозначая недобор отрицательными числами, а результаты с запасом — положительными.

Итак, 81 − 92 = −11; 98 − 92 = 6; 90 − 92 = −2; 93 − 92 = 1.

Сложив эти числа, получаем корректировку для необходимого минимума: −11 + 6 − 2 + 1 = −6.

Получается дефицит в 6 баллов, а значит, необходимый минимум увеличивается: 92 + 6 = 98. Дела плохи. 🙁